c#约瑟夫环
约瑟夫环是一个数学的应用问题:已知n个人(以编号1,2,3…n分别表示)围坐在一张圆桌周围。从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列;依此规律重复下去,直到圆桌周围的人全部出列。
例如:
n = 9, k = 1, m = 5
【解答】
出局人的顺序为5, 1, 7, 4, 3, 6, 9, 2, 8。
约瑟夫环是一个数学的应用问题:已知n个人(以编号1,2,3…n分别表示)围坐在一张圆桌周围。从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列;依此规律重复下去,直到圆桌周围的人全部出列。
例如:
n = 9, k = 1, m = 5
【解答】
出局人的顺序为5, 1, 7, 4, 3, 6, 9, 2, 8。
关于C#窗体间的数据传值的方法好几种,在项目中都各有应用,虽然简单,这里记录下来,分享给大家!
主窗体
1 | private void button_Click(object sender, System.EventArgs e) |
子窗体(Form2)
最近做信息安全方面的项目,看到一些关于混沌变换的论文,总结一番。
如果一个系统的演变过程对初始的状态十分敏感,就把这个系统称为是混沌系统。
在1972年12月29日,美国麻省理工教授、混沌学开创人之一E.N.洛仑兹在美国科学发展学会第139次会议上发表了题为《蝴蝶效应》的论文,提出一个貌似荒谬的论断:在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个龙卷风,并由此提出了天气的不可准确预报性。至此以后,人们对于混沌学研究的兴趣十分浓厚,今天,伴随着计算机等技术的飞速进步,混沌学已发展成为一门影响深远、发展迅速的前沿科学。
混沌来自于非线性动力系统,而动力系统又描述的是任意随时间变化的过程,这个过程是确定性的、类似随机的、非周期的、具有收敛性的,并且对于初始值有极敏感的依赖性。而这些特性正符合序列密码的要求。19**Robert Matthews在Logistic映射的变形基础上给出了用于加密的伪随机数序列生成函数,其后混沌密码学及混沌密码分析等便相继发展起来。混沌流密码系统的设计主要采用以下几种混沌映射:一维Logistic映射、二维He’non映射、三维Lorenz映射、逐段线性混沌映射、逐段非线性混沌映射等,在本文中,我们主要探讨一维Logistic映射的一些特性。
“恺撒密码”据传是古罗马恺撒大帝用来保护重要军情的加密系统。(即今天我们所说的:替代密码)
它是一种代换密码,通过将字母按顺序推后起3位起到加密作用,如将字母A换作字母D,将字母B换作字母E。据说恺撒是率先使用加密函的古代将领之一,因此这种加密方法被称为恺撒密码。
假如有这样一条指令:
明文(小写):ji xiao jing
用恺撒密码加密后就成为:
上篇显示了用错误的key得到了错误的结果,现在使用正确的key
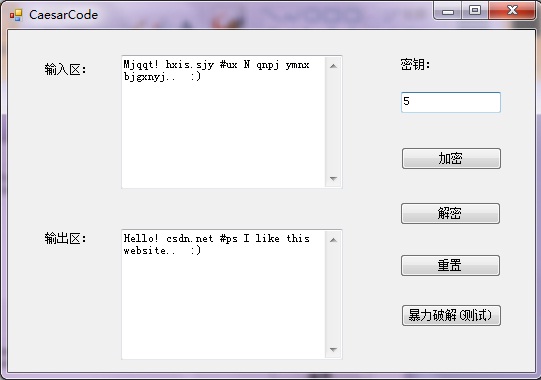
这样就得到了正确的结果。
当然,这个程序只是演示凯撒密码的一个思路,没有对其他符号加密,这样有个很严重的后果,就是很key容易被破解。
举例:(key是*不告诉你,嘿嘿)
自动填表的方式有很多,关键是获取控件的id或者name。
比如源代码有
1 | <input id="pwdInput" tabindex="2" class="ipt-t" type="password" name="password" onMouseOver="fEvent('mouseover',this)" onFocus="fEvent('focus',this)" onBlur="fEvent('blur',this)" onMouseOut="fEvent('mouseout',this)"/> |
那么就可以用
1 | HtmlDocument doc = webBrowser1.Document; |
1 | private MouseButtons Button; |
1 | using System; |
1 | using System; |
开发类似千千静听或者KMplayer等音频视频播放器播放字幕或者歌词的技术
从两方面着手,一是时间轴,二是帧(对于视频)。
方法一的实现比较简单,只需要内置一个定时器,在媒体播放时开始计时,然后读指定的脚本即可。
1 | using System; |
方法二需要利用DirectX开发,或者flash播放的技术拆解成帧然后播放
1 | using System.Diagnostics; |